Quick Look
Grade Level: 7 (6-8)
Time Required: 1 hour
Lesson Dependency: None
Summary
The concept of geocaching is introduced as a way for students to explore using a global positioning system (GPS) device and basic geographic information (GIS) skills. Students familiarize themselves with GPS, GIS, and geocaching as well as the concepts of latitude and longitude. They develop the skills and concepts needed to complete the associated activity while considering how these technologies relate to engineering. Students discuss images associated with GPS, watch a video on how GPS is used, and review a slide show of GIS basics. They estimate their location using latitude and longitude on a world map and watch a video that introduces the geocaching phenomenon. Finally, students practice using a GPS device to gain an understanding of the technology and how location and direction features work while sending and receiving data to a GIS such as Google Earth.Engineering Connection
Civil, petroleum and environmental engineers, and many others, use GPS and GIS to analyze data and make informed decisions. Some civil engineers use GPS and GIS in large-scale urban planning projects. Some petroleum engineers map the extent of rock outcroppings known to contain oil or gas deposits by using GPS devices to map the outcropping surface and using GIS to integrate other data into the map. Environmental engineers may use these tools to map water resources and study climate change. This lesson demonstrates another important connection between engineering and math—problem solving—as students break up larger composite shapes into smaller shapes in order to simplify their calculations.
Learning Objectives
After this lesson, and its associated activity, students should be able to:
- Determine a latitude and longitude from a map.
- Operate a GPS device.
- Identify location by its latitude and longitude.
- Create a waypoint.
- Use compass and distance features.
Worksheets and Attachments
Visit [www.teachengineering.org/curriculum/print/uow-2262-integrating-gis-mathematics-engineering-gps] to print or download.Pre-Req Knowledge
Familiarity with calculating the area of regular and irregular shapes, finding missing angle measurements, and complementary and supplementary angles.
Introduction/Motivation
At any given moment, thousands of satellites orbit the Earth. In fact, on any clear, cloudless night away from city lights, you may be able to look up and spot a satellite or two passing overhead!
The satellites are used for many purposes: military, data collection, communication, weather. One famous satellite is the Hubble Space Telescope—a vital research tool that does not look at the Earth, but instead scans the darkness of space to study our universe. One of the most important satellites is a group of satellites that compose a navigation system called the global positioning system, commonly known as GPS. This satellite-based system—developed by the U.S. government for military use in the 1970s, and later for civilian use in the 1980s—provides information about position and location to users around the globe, including you!

We can use GPS through GPS-enabled devices, such as car navigation systems and smartphone apps. Most commonly, apps like Google Maps or Apple Maps use GPS to help everyday users with driving directions or location finding. However, GPS has a wide range of commercial and business applications, particularly in engineering. Civil engineers use GPS to survey and plan community infrastructure projects. Aerospace engineers incorporate GPS in aircraft and rocket design to assist with navigation. Environmental engineers employ GPS to gather data on geographic locations and the wildlife contained within them.
Before we dive deeper into other applications of GPS, let’s take a look at the following questions and see if we can answer them.
What is GPS? What does it do?
- GPS stands for global positioning system.
- It helps you pinpoint your location, usually on a map.
What would you used GPS for?
- GPS is used via a GPS-enabled device and a software application interface to obtain driving directions, plot a course, or find a location or waypoint on a map.
Why would engineers put GPS capability on a rocket? (Show students the rocket image below.)
- To make sure it doesn’t land somewhere dangerous and arrives at its intended destination.

What kind(s) of engineers are needed to design and launch rockets?
- So many types! For example, aerospace, mechanical, materials, chemical, computer and software engineers.
Why do you think people/engineers might want to monitor the location of animals, such as wolves? (Show the wolf image below.)
- To monitor their migration habits, check on the health of animals released after medical treatment, and track endangered species.

Why might engineers need to know locations on earth? How about locations in space?
- To study a given area and help humans utilize the resources
- To collect data
- To help improve the world
- To navigate effectively and to avoid other space objects
(As either an introduction or lesson supplement, consider showing students one of the following TEDx Talk videos: Geographic Information Systems (GIS): Dan Scollon at TEDxRedding; from sciBRIGHT, How Does GPS Work?; or from Esri, What is GIS? Also, introduce students to the PDF titled The Fundamentals of GIS and Real-World Applications Handout and go over it throughout the lesson.)
Introducing GIS
If any of you have used a navigation app such as Google Maps, then you have used a GIS—even if you were not aware of it!
To understand GIS and GPS, we must first understand how we mark locations on the earth. People use a GPS-enabled device to identify their locations using latitude and longitude. Latitude and longitude are like the x- and y-axes on the coordinate plane. To picture this, imagine unrolling the earth's surfaace and making it flat, like a paper map. Then, overlay a grid of axes over the map (as in Figure 1). The lines that identify your location from north to south we call lattitude. The lines that represent your location from east to west we call longitude. The equator—a horizontal line that passes through South America, sub-Saharan Africa, and much of Indonesia—represents the x-axis: 0° north and south, while the prime meridian—a vertical line passing through the UK—represents the y-axis: 0° east and west.
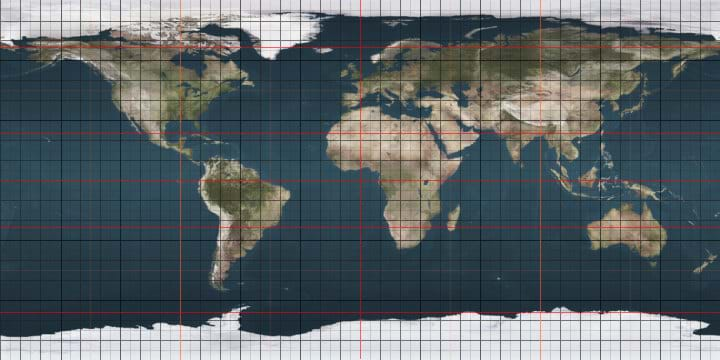
One example using latitude and longitude is to determine the approximate center of the lower 48 U.S. states, located at (latitude) 39.8° north and (longitude) 98.6° west near Lebanon, KS.
Now, estimate the location of your school using this latitude and longitude map. During the next part of the lesson, we will check our estimates with real GPS coordinates. You can also estimate coordinates on a physical map in the classroom, such as one from National Geographic. Just remember, for latitude, include the degree symbol ° and “north” or “south.” For longitude, include the degree symbol ° and “east” or “west.”
Geocaching

One fascinating and fun use of GPS and GIS technologies is a hobby called “geocaching.” This is a treasure-hunting activity that takes place worldwide and is open to everyone who has a sense of adventure and a GPS device or smartphone! Let's watch this short video, “What is Geocaching,” to learn more about this real-world adventuring that is happening right now all around you.
We are going to work with geocaches using our own GPS devices during a future activity, all while exploring what it would be like to be an engineer using GIS and GPS!
GPS Hardware and GIS Software
In preparation for the activity, we will practice:
- Creating and sending a waypoint to Google Earth
- Determining your distance from a waypoint
- Navigating to and from the waypoint
- Following a compass bearing
Below are screen captures from the Apple iOS software. For the purposes of this tutorial, the following instructions are for the “Free GPS” app, available on the iOS platform. Alternate GPS apps are available for Android operating systems, such as “Maverick: GPS Navigation” and “Handy GPS.” Google Earth is available for both iOS and Android from the App Store and Google Play. You can also use a desktop version of Google Earth to export or email waypoint data from a smartphone.
Example—How to Create and Send Waypoints to Google Earth:
The main screen in the Free GPS app shows your compass bearing and the distance from a chosen waypoint (as shown in Figure 2).
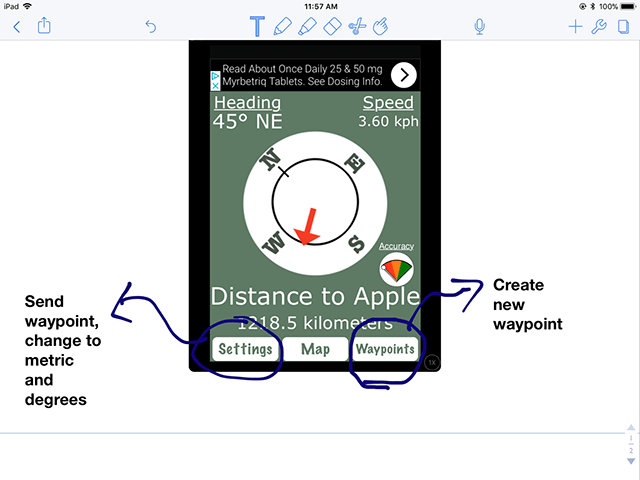
Open the Free GPS app. To create a waypoint, simply click on “Waypoints” and then “Add Waypoint.” If you are in the location you want to use, click on “Add Current Position” to use your current position for the new waypoint. This will enable you to see the latitude and longitude of your location, and change the name of the waypoint. See Figure 3.

Take note of your location in latitude and longitude of the classroom as an example. Again, for latitude remember to include the degree symbol ° and “north” or “south.” For longitude, include the degree symbol ° and “east” or “west.”
To send a waypoint from this app to Google Earth, simply go to “Settings” and click “Email Waypoints." See Figure 4.
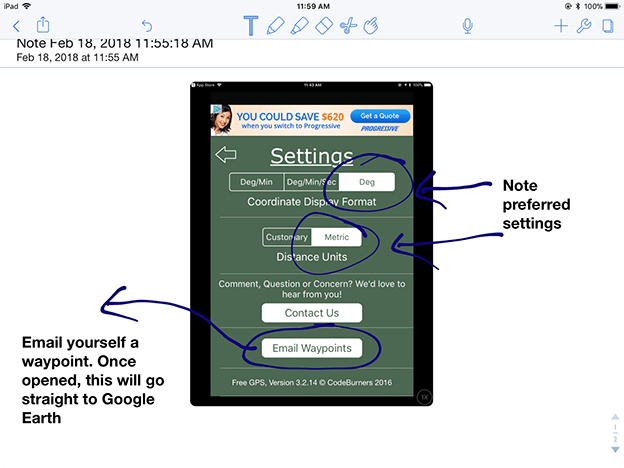
Open Google Earth on a computer. Then open the file from the email on your computer and notice how it appears in Google Earth.
Next, we will walk around the room to experience how the distance and compass functions work. On the main screen, the app shows how far you have walked from the waypoint you created originally. You will use a feature like this in the activity. Be sure you hold the device flat, parallel to the ground. Notice as you move, so does the compass, showing your heading facing straight in front of the device. You will also need to use this compass bearing during the activity. Here is a helpful chart to familiarize yourself with compass headings and how they relate to north, south, east, and west (sketch this table on the classroom board).
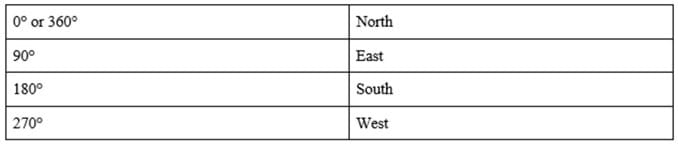
(Once students are familiar with the app, move on to conduct the Geometry and Geocaching Using GIS and GPS activitiy.)
Lesson Background and Concepts for Teachers
Geographic information systems (GIS) integrate data from a wide variety of fields—natural sciences, social sciences, and engineering—and display data in map form. The global positioning system (GPS) is a global satellite-based navigation array that provides location and time information to GPS receivers anywhere on or near the Earth, provided the device has a line of sight to four or more GPS satellites. GIS and GPS go hand-in-hand as much of the data used in GIS is obtained with GPS coordinates to pinpoint locations based on data.
Geocaching is a hobby in which people hide items around the world and post instructions on how to find them. Then, other geocache hunters use GPS-enabled devices to find the hidden cache, or treasure. GPS devices display a user’s location on a map from which they can save their locations and upload the data to a computer. Many devices have GPS receivers embedded within them, such as smartphones as well as technology used in engineering like surveying equipment. Students take the role of a geocache hunter, using a GPS-enabled device to locate a certain point on the Earth’s surface. They use hints at each waypoint to find other locations. When mapped out on Google Earth, they can visualize the length and direction of where they traveled. Refer to the Topographic Maps and Ratios: A Study of Denali activity for students to discover how to use map scales as ratios to navigate a map.
Engineers of all types use GPS and GIS to acquire, compile, and view data so they may make informed decisions throughout their problem-solving process. This lesson introduces students to GIS and GPS through the lens of geocaching while practicing other concepts like geometry and scale. Students need to be familiar with calculating area of regular and irregular shapes, finding missing angle measures, and understanding complementary and supplementary angles. The lesson is also suitable for use in conjunction with rate and unit rate concepts.
Most free GPS apps are quite user friendly and can be used by individuals with limited knowledge of GPS and GIS. This lesson uses one example of a free GPS app available for iOS. If you decide to use another application (for example, on an Android device), you must know how to send waypoints to Google Earth via email in the form of KML files (also known as keyhole markup language—a computer text language that expresses geographic annotation and visualization). If the KML file does not load in Google Earth, click and directly drag the file into Google Earth from its folder wherever you chose to save it. To do this, release the mouse pointer over the map portion of Google Earth.
Most GPS software provides a way for users to send waypoints to Google Earth as KML files. Make sure the teachers and students understand the GPS software of the devices used in the classroom.
Before undertaking this lesson and its associated activities, it is recommended that the teacher become familiar with the technologies—both GPS and GIS (Google Earth). For more information on teacher preparation, refer to the Geometry and Geocaching Using GIS and GPS activity.
Lesson Closure
What is GIS? What is GPS? How are they related? How does geocaching use these technologies? Why might different types of engineers want to use GIS and GPS in their jobs? When do you use GIS in your daily activities? What are latitude and longitude?
Vocabulary/Definitions
coordinate: The combination of longitude and latitude, along with elevation, make a GPS coordinate which defines a single point on the surface of the earth.
geographic information system: A way to store, edit, and manipulate data or information, usually using maps; commonly referred to as GIS.
global positioning system: A satellite based navigation system that allows users to determine their position on the earth, among other uses; commonly referred to as GPS. More broadly, GPS can refer to any device used to locate a given position.
latitude: This represents an angle north or south of the equator, but is more easily understood as the y-coordinate of a location on the surface of the earth.
longitude: This represents an angle east or west of the prime meridian, but is more easily understood as the x-coordinate of a location on the surface of the earth.
waypoint: In the case of navigation, a fixed longitudinal and latitudinal coordinate or GPS point that identify a physical point.
Assessment
Pre-Lesson Assessment
Turn and Talk: Conduct a class discussion prompted by the following questions. Students' answers and comments reveal their base understanding of the lesson topic.
- What is GPS?
- What is GIS?
- Have you ever used either?
- Can you think of any type of engineer who might use either?
Post-Introduction Assessment
Re-Visit Turn and Talk: Ask the same discussion questions again after presenting and completing the Introduction/Motivation section as a way to gauge how much information students learned.
Lesson Summary Assessment
Researching Engineers: Based on their knowledge of GPS, GIS, and geocaching, discuss as a class the types of engineers that may use these geographic information tools. Prompt students with the following career paths:
- Civil engineer
- Mechanical engineer
- Energy systems engineer
- Biomedical engineer
- Geologic engineer
- Another engineer type of your choice (check with teacher first)
Homework
Activity Prep: Have students prepare for the associated activity by either downloading a free GPS app and creating at least three waypoints on their way home from school (if they have access to their own smartphones). Or, create an assignment using The Fundamentals of GIS and Real-World Applications Handout such as exploring Google Earth or finding a particular set of latitudes and longitudes on a traditional 2D/paper map.
Lesson Extension Activities
Give students time to research different types of engineers. Either assign students to individually research and write about these career types, or present their findings in small groups.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!References
Katrina Patton. The Fundamentals of GIS and Real World Application (PDF). University of Western Wyoming. https://www.teachengineering.org/content/uow_/lessons/uow-2262-integrating-GIS/uow-2262-integrating-GIS-fundamentals-of-GIS-handout.pdf
Using Your iPhone & Google Earth for Plot Mapping (PDF). University of California Davis. http://wrir4.ucdavis.edu/Resources/Tricks/docs/GPS-GoogleEarth%20Plot%20Mapping-iPhone.pdf
Other Related Information
Find additional interesting lessons about GIS in TeachEngineering by searching with "GIS" as a keyword. Most of these lessons and their associated activities involve data, maps, and projections, and are great activities to conduct in association with this lesson (see list below). However, this lesson and activity deals with a different niche that is not available in other lessons: the hands-on use of a GPS device and its integration with GIS is unique.
Other relevant lessons and activities at TeachEngineering.org:
Projections and Coordinates: Turning a 3D Earth into Flatlands
Copyright
© 2018 by Regents of the University of Colorado; original © 2017 University of WyomingContributors
Jake Schell; Andrea BurrowsSupporting Program
University of WyomingAcknowledgements
This digital library curriculum was developed under the guidance of Andrea Burrows, Linda Hutchinson, and Michele Chamberlin at the University of Wyoming.
Last modified: June 10, 2019













User Comments & Tips